Signals and Systems - Section 1 (5)
- Home
- Electronics & Communication Engineering
- Electronics and Communication Engineering
- Signals and Systems - Section 1
Signals and Systems - Section 1
| 33. | Laplace transform of a pulse function of magnitude E and duration from t = 0 to t = a is |
|||||||
|
| 34. | Which one is a linear system? |
|||||||
Answer: Option B Explanation: For linearity y1[n] = x1[n] + x2[n - 10] ...(1) y2 = x2[n] + x2[n - 10] ...(2) y1[n] = x1[n] + x2[n] + x2[n - 10] + x2[n - 10] ...(3) Now find y1[n] + y2[n] Corresponding to x1[n] + x2[n] It is same as equation (3) hence linear. But in part (c) y[n] = x2[n] ⇒ y1[n] = x21[n], y2[n] = x22[n]⇒ y1[n] + y2[n] = x22[n]...3 But y1[n] + y2[n] Corresponing x1[n] + x2[n] is y1[n] + y2[n] = {x1[n] + x2[n]}2 = x12[n] + x22[n] + 2x1[n] x2[n]....4 Equations (3) and (4) are not same hence not linear. |
| 35. | Let x(t) and y(t) with F.T. x(f) and y(f) respectively be related as shown in figure Then y(f) is |
|||||||
Answer: Option B Explanation: By applying time shifting and scaling property. |
| 37. |
|
|||||||
Answer: Option A Explanation: H(z) = 6 + z-1 - z-2, solve it by considering H(z) = 0 z = 1/3, -1/2 in H(z) only numerator. Hence z = 1/3, - 1/2 will be zero, and if zero lies inside the unit circle, system will be of minimum phase. |
| 38. | A pole zero pattern of a certain filter is shown in figure. This filter must be |
|||||||
Answer: Option D Explanation: In transfer function, no of zeros = no. of poles, hence it is all pass fliter. |
| 39. | The system with given pole-zero diagram is |
|||||||
Answer: Option D Explanation: Because no.of zero is more than Pole, therefore when you find transfer function. Numerator power will higher than denominator, and such transfer functions is not realizable. |
| 40. | The z-transform of a particular signal is given The system after implementation will be |
|||||||
|

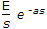
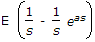
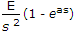
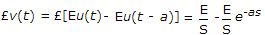

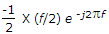

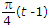 is
is








