Height and Distance - General Questions
| 1. | The angle of elevation of the sun, when the length of the shadow of a tree √3 times the height of the tree, is: |
||||||||||||
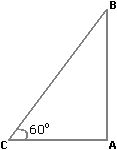
Answer: Option A Explanation: Let AB be the tree and AC be its shadow.
Let
|
ACB = 
.
cot 
| 2. | From a point P on a level ground, the angle of elevation of the top tower is 30°. If the tower is 100 m high, the distance of point P from the foot of the tower is: |
||||||||||||||||||||
Answer: Option C Explanation: Let AB be the tower.
Then,
|
| 3. | An observer 1.6 m tall is 203 away from a tower. The angle of elevation from his eye to the top of the tower is 30°. The height of the tower is: |
||||||||||||||||
Answer: Option A Explanation: Let AB be the observer and CD be the tower.
Draw BE Then, CE = AB = 1.6 m, BE = AC = 203 m.
|
CD.| 4. | The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is: |
||||||||||||||||||
Answer: Option D Explanation: Let AB be the wall and BC be the ladder.
Then,
|
| 5. | A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30° with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60°. What is the distance between the base of the tower and the point P?
|
|||||||||
Answer: Option D Explanation: One of AB, AD and CD must have given.
So, the data is inadequate. |
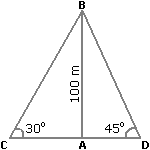
| 6. | Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is: |
||||||||||||||||||||||||
Answer: Option C Explanation: Let AB be the lighthouse and C and D be the positions of the ships.
Then, AB = 100 m,
|
